Statistical modelling

" />

# Statistical modelling
## A grossly inadequate introduction
### Danielle Navarro     @djnavarro
### <a href="https://djnavarro.github.io/chdss2018/" class="uri">https://djnavarro.github.io/chdss2018/</a> 11 December 2018

---

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
tinyframes <- frames %>%
 group_by(id, age, condition) %>%
 summarise(
 response = mean(response)
 ) %>%
 ungroup()
```

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

# Simplified data set

- Average all responses by an individual
- Ignores effect of number of observations
- Each person provides one "average response"
- Impoverished, but easy to analyse!

]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
tinyframes <- frames %>%
 group_by(id, age, condition) %>%
 summarise(
 response = mean(response)
 ) %>%
 ungroup()

*tinyframes
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## # A tibble: 225 x 4
## id age condition response
## <int> <int> <chr> <dbl>
## 1 1 36 category 5.33
## 2 2 46 category 7.05
## 3 3 33 property 4.86
## 4 4 71 property 3.86
## 5 5 23 property 9 
## 6 6 31 category 7.90
## 7 7 23 property 3.76
## 8 8 31 property 4 
## 9 9 37 category 3.38
## 10 10 46 category 5.86
## # ... with 215 more rows
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
tinyframes <- frames %>%
 group_by(id, age, condition) %>%
 summarise(
 response = mean(response)
 ) %>%
 ungroup()

tinyframes %>%
  group_by(condition) %>%
  summarise(
*   mean_resp = mean(response),
*   sd_resp = sd(response),
*   n = n()
  )
```
]]]
]]
--
.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## # A tibble: 2 x 4
## condition mean_resp sd_resp n
## <chr> <dbl> <dbl> <int>
## 1 category 5.40 1.56 114
## 2 property 4.39 1.37 111
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
tinyframes %>% 
  ggplot(aes(
    x = age, 
    y = response, 
    colour = condition)) + 
* geom_smooth(method = "lm") +
  geom_point()
```

- Is this difference meaningful?
- What tools do we use to assess it?

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[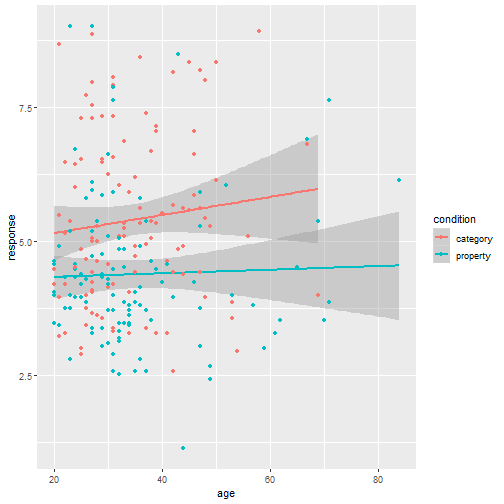
![](statistics-slides_files/figure-html/plottinyfrmaes-1.png)

]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
t.test(
  formula = response ~ condition, 
  data = tinyframes, 
  var.equal = TRUE
)
```

- The answer we were taught.
    - H0: same mean
    - H1: different mean
    - etc, etc

]]]
]]
--
.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## 
## 	Two Sample t-test
## 
## data:  response by condition
*## t = 5.1625, df = 223, p-value = 5.388e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.6259535 1.3988834
## sample estimates:
## mean in group category mean in group property 
##               5.397661               4.385242
```

- Yay the magic p<.05. Winning!

]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
t.test(
  formula = response ~ condition, 
  data = tinyframes, 
  var.equal = TRUE
)
```

- The answer we were taught.
    - H0: same mean
    - H1: different mean
    - etc, etc

]]]
]]
.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## 
## 	Two Sample t-test
## 
## data:  response by condition
## t = 5.1625, df = 223, p-value = 5.388e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
*##  0.6259535 1.3988834
## sample estimates:
## mean in group category mean in group property 
##               5.397661               4.385242
```

- Effect size? 
    - I'm not a fan of "standardised" effect size
    - 95% CI for the difference in raw scores...
    - ...it's about 1 point on the 9 point scale
    - divide by std. dev if you want Cohen's d
    
]]]
]]

---
class: bg-main1 center middle hide-slide-number

.reveal-text.bg-main2[.pad1[
.font4[Linear models]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

Linear models:

`$\mu_i = b_0 + b_1 X_1 + b_2 X_2 + ... + b_k X_k$` 
`$Y_i \sim \mbox{Normal}(\mu_i, \sigma)$`

]]]
]]

.row.bg-main3[.content.vtop.center[
![](statistics-slides_files/figure-html/unnamed-chunk-7-1.png)
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

Linear models in R:

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
```
]]]
]]

.row.bg-main3[.content.vtop.center[
![](statistics-slides_files/figure-html/unnamed-chunk-9-1.png)
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
Inspecting linear models in R:

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
mod2 
```
]]]
]]
--
.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## 
## Call:
## lm(formula = response ~ condition, data = tinyframes)
## 
## Coefficients:
##       (Intercept)  conditionproperty  
*##             5.398             -1.012
```

- Hey those numbers look familiar
- Relationship to t.test?

]]]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

Comparing linear models with F-tests:

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
*anova(mod1, mod2)
```
]]]
]]
--
.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Analysis of Variance Table
## 
## Model 1: response ~ 1
## Model 2: response ~ condition
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    224 539.98                                  
*## 2    223 482.33  1    57.645 26.652 5.388e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]]]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[
Comparing several linear models with F-tests:

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
*mod3 <- lm(formula = response ~ condition + age, data = tinyframes)
*anova(mod1, mod2, mod3)
```
]]]
]]

.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Analysis of Variance Table
## 
## Model 1: response ~ 1
## Model 2: response ~ condition
## Model 3: response ~ condition + age
##   Res.Df    RSS Df Sum of Sq       F    Pr(>F)    
## 1    224 539.98                                   
*## 2    223 482.33  1    57.645 26.6544 5.399e-07 ***
*## 3    222 480.12  1     2.214  1.0238    0.3127    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]]]
]]

---
class: bg-main1 center middle hide-slide-number

# Why do I care about F-tests again????
 
<img src="images/adaY.png" width="60%">

---
class: bg-main1 center middle

.pull.left[.pad1[.font2[
# Eh. Let's skip the rant and jump to... TL;DR:

What problem are you trying to solve?
- Hypothesis testing vs estimation?
- Bayesian inference vs frequentist?
- Exploration vs confirmation?
- Decision making vs learning?

Different problems lead to different statistics 
Orthodox null hypothesis tests are *specific* tools
]]]

---
class: bg-main1 center middle

.pull.left[.pad1[.font2[
# Eh. Let's skip the rant and jump to... TL;DR:

What problem are you trying to solve?
- .orange[Hypothesis testing] vs estimation?
- Bayesian inference vs .orange[frequentist]?
- Exploration vs .orange[confirmation]?
- .orange[Decision making] vs learning?

Different problems lead to different statistics 
.orange[Orthodox null hypothesis tests] are *specific* tools
]]]

---
class: bg-main1 center middle

.pull.left[.pad1[.font2[
# Eh. Let's skip the rant and jump to... TL;DR:

What problem are you trying to solve?
- .blue[Hypothesis testing] vs estimation?
- .blue[Bayesian inference] vs frequentist?
- Exploration vs .blue[confirmation]?
- Decision making vs learning.blue[???]

Different problems lead to different statistics 
.blue[Bayes factors] are *specific* tools
]]]

---
class: bg-main1 center middle

.pull.left[.pad1[.font2[
# Eh. Let's skip the rant and jump to... TL;DR:

What problem are you trying to solve?
- Hypothesis testing vs .yellow[estimation]?
- .yellow[Bayesian inference] vs frequentist?
- .yellow[Exploration] vs confirmation?
- Decision making vs .yellow[learning]

Most of .yellow[my modelling problems] are this! 
:-)
]]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[
Akaike Information Criterion?

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
mod3 <- lm(formula = response ~ condition + age, data = tinyframes)
*AIC(mod1, mod2, mod3)
```
]]]
]]
--
.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

```
##      df      AIC
## mod1  2 839.4940
*## mod2  3 816.0928
## mod3  4 817.0575
```
]]]
]]

---
class: split-40 bg-main3

.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[
Bayesian information criterion?

```r
mod1 <- lm(formula = response ~ 1, data = tinyframes) 
mod2 <- lm(formula = response ~ condition, data = tinyframes)
mod3 <- lm(formula = response ~ condition + age, data = tinyframes)
*BIC(mod1, mod2, mod3)
```
]]]
]]
--
.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
##      df      BIC
## mod1  2 846.3262
*## mod2  3 826.3411
## mod3  4 830.7219
```
]]]
]]

---
class: split-50 bg-main1

.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[
Bayes factors?

```r
library(BayesFactor)
tf <- as.data.frame(tinyframes)
mod2b <- lmBF(formula = response ~ condition, data = tf)
mod3b <- lmBF(formula = response ~ condition + age, data = tf)
*mod2b / mod3b
```
]]]
]]
--
.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Bayes factor analysis
## --------------
*## [1] condition : 4.376014 ±1.64%
## 
## Against denominator:
##   response ~ condition + age 
## ---
## Bayes factor type: BFlinearModel, JZS
```
]]]
]]

---
class: bg-main1 center middle hide-slide-number

.reveal-text.bg-main2[.pad1[
.font4[Linear mixed models 1]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes <- frames %>% 
 group_by(
 id, age, condition, n_obs) %>%
 summarise(
 response = mean(response)) %>%
 ungroup()

modestframes
```

- But what if I care about how people adjust their beliefs as more data arrive? 
- If so, I don't want to collaps "n_obs", I want to analyse it

]]]
]]

--
.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## # A tibble: 675 x 5
## id age condition n_obs response
## <int> <int> <chr> <int> <dbl>
## 1 1 36 category 2 5.86
## 2 1 36 category 6 5.29
## 3 1 36 category 12 4.86
*## 4 2 46 category 2 5.29
*## 5 2 46 category 6 7.57
*## 6 2 46 category 12 8.29
## 7 3 33 property 2 5.43
## 8 3 33 property 6 4.86
## 9 3 33 property 12 4.29
## 10 4 71 property 2 4.57
## # ... with 665 more rows
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
whichids <- modestframes %>%
 pull(id) %>%
 unique() %>%
 sample(size = 80)

whichids
```

- Pick a random subset of 80 people...
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
##  [1] 216 206  61  45 143 175  71 186  24 178  50 122 184 219 220  26   2
## [18]  88 200  36 147 211  35  55 132   8 109 102  25 119  96   6  23 212
## [35]  12 214  76  13 169  39  57  53  91  46 162 199 145 148 183 136  82
## [52]  67   4 117 141  49  81 110 170  11  29 207 127 174  99  94  51 120
## [69] 209 108  89  42  77  73 100 153  60 204  48   7
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
whichids <- modestframes %>%
 pull(id) %>%
 unique() %>%
 sample(size = 80)

modestframes %>%
  filter(id %in% whichids) %>%
  ggplot(aes(
    x = n_obs, y = response, 
    colour = factor(id))) +
  geom_point(
    show.legend = FALSE,
    size = 8) + 
  geom_line(
    show.legend = FALSE, 
    alpha = .3) + 
  facet_wrap(~ condition)
```

- ...and plot their responses
]]]
]]

--
.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[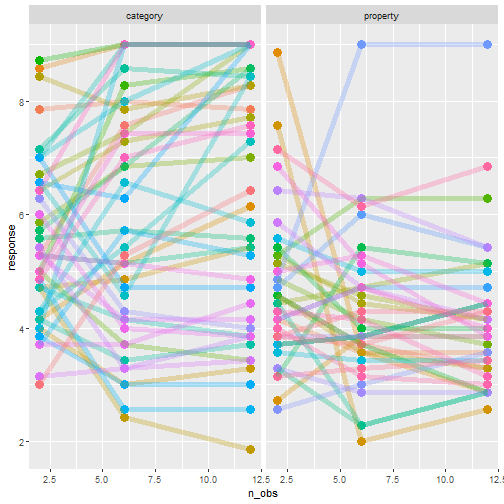
![](statistics-slides_files/figure-html/plotmodest-1.png)
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
Thoughts:
- Systematic trend?
- Not the same in each condition?
- Not homogenous across people?

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[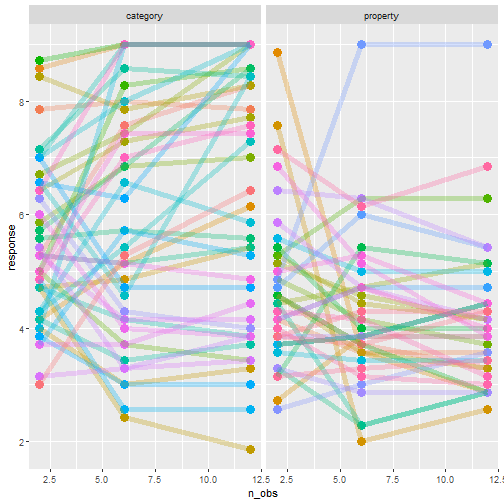
![](statistics-slides_files/figure-html/plotmodest2-1.png)
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
Thoughts:
- Systematic trend?
- Not the same in each condition?
- Not homogenous across people?

Tools?
- Repeated measures ANOVA?
- MANOVA?
- .orange[Linear mixed model]

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[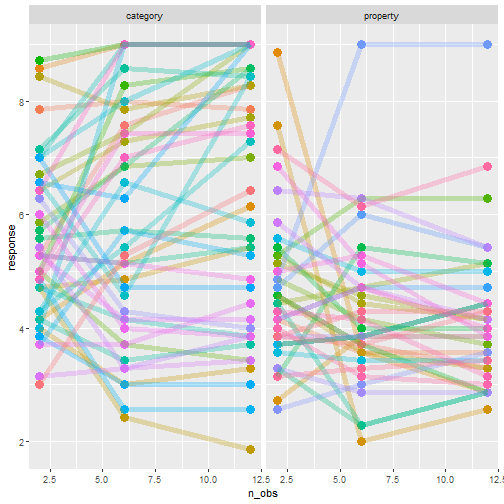
![](statistics-slides_files/figure-html/plotmodest3-1.png)
]]]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
Repeated measures ANOVA as a mixed model:

```r
modest1 <- lmer(formula = response ~ 1 + (1|id), data = modestframes)
modest2 <- lmer(formula = response ~ condition + n_obs + (1|id), data = modestframes)

anova(modest1, modest2)
```
]]]
]]
--
.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Data: modestframes
## Models:
## modest1: response ~ 1 + (1 | id)
## modest2: response ~ condition + n_obs + (1 | id)
##         Df    AIC    BIC  logLik deviance  Chisq Chi Df Pr(>Chisq)    
## modest1  3 2354.9 2368.5 -1174.5   2348.9                             
## modest2  5 2333.5 2356.1 -1161.8   2323.5 25.403      2  3.046e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
But RM-ANOVA is absurd!!!

Traditional RM-ANOVA allows:
- random effect for intercept
- fixed effects

It doesn't do:
- random slopes of conditions
- so you have to believe all these lines are "really" the same slope...

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[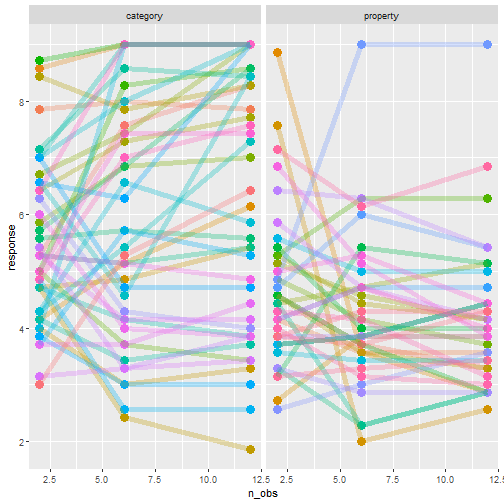
![](statistics-slides_files/figure-html/plotmodest4-1.png)
]]]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

```r
modest1 <- lmer(formula = response ~ 1 + (1|id), data = modestframes)
modest2 <- lmer(formula = response ~ condition + n_obs + (1|id), data = modestframes)
*modest3 <- lmer(formula = response ~ condition + n_obs + (1 + n_obs|id), data = modestframes)

anova(modest1, modest2, modest3)
```
]]]
]]

--
.row.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Data: modestframes
## Models:
## modest1: response ~ 1 + (1 | id)
## modest2: response ~ condition + n_obs + (1 | id)
*## modest3: response ~ condition + n_obs + (1 + n_obs | id)
##         Df    AIC    BIC  logLik deviance  Chisq Chi Df Pr(>Chisq)    
## modest1  3 2354.9 2368.5 -1174.5   2348.9                             
## modest2  5 2333.5 2356.1 -1161.8   2323.5 25.403      2  3.046e-06 ***
*## modest3  7 2270.4 2302.0 -1128.2   2256.4 67.164      2  2.603e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
summary(modest3)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
...
## Linear mixed model fit by REML ['lmerMod']
## Formula: response ~ condition + n_obs + (1 + n_obs | id)
##    Data: modestframes
## 
*## REML criterion at convergence: 2267.9
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.8960 -0.3681 -0.0306  0.3557  3.3860 
## 
...
```

- Terminology:
    - ML: Maximum likelihood
    - REML: Restricted maximum likelihood
- What's the difference?
    - ML: Fit everything at once
    - REML: Fit fixed first, then fit random
]]]

]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
summary(modest3)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
...
## Linear mixed model fit by REML ['lmerMod']
## Formula: response ~ condition + n_obs + (1 + n_obs | id)
##    Data: modestframes
## 
## REML criterion at convergence: 2267.9
## 
## Scaled residuals: 
*##     Min      1Q  Median      3Q     Max 
*## -2.8960 -0.3681 -0.0306  0.3557  3.3860 
## 
...
```

- This is pointless
- Yes, it's **very** important to look at residuals
- But this summary is unreadable
- Just plot them (coming soon!)
]]]

]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
summary(modest3)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
...
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
##  id       (Intercept) 1.72618  1.3138        
##           n_obs       0.01684  0.1298   -0.21
##  Residual             0.55277  0.7435        
## Number of obs: 675, groups:  id, 225
## 
## Fixed effects:
##                     Estimate Std. Error t value
*## (Intercept)        5.2256978  0.1385646  37.713
*## conditionproperty -0.6693767  0.1874783  -3.570
*## n_obs              0.0004094  0.0111058   0.037
## 
...
```

- Estimated average effect of condition is about .7?
- Estimated average effect of n_obs exists, but is small?
- Don't forget: this is raw scale (condition: 0-1, n_obs: 2-12)

]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
summary(modest3)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
...
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
*##  id       (Intercept) 1.72618  1.3138        
*##           n_obs       0.01684  0.1298   -0.21
##  Residual             0.55277  0.7435        
## Number of obs: 675, groups:  id, 225
## 
## Fixed effects:
##                     Estimate Std. Error t value
## (Intercept)        5.2256978  0.1385646  37.713
## conditionproperty -0.6693767  0.1874783  -3.570
## n_obs              0.0004094  0.0111058   0.037
## 
...
```

- Random effects (presumed normal, mean zero)
- Random effects look quite variable, so take care
- Looks like slope & intercept are correlated (grossly typical)

]]]
]]

---
class: split-30 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes$modelfit <- predict(modest3)
modestframes$resid <- residuals(modest3)
modestframes
```
]]]
]]

--
.row.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## # A tibble: 675 x 7
## id age condition n_obs response modelfit resid
## <int> <int> <chr> <int> <dbl> <dbl> <dbl>
## 1 1 36 category 2 5.86 5.55 0.310 
## 2 1 36 category 6 5.29 5.33 -0.0479
## 3 1 36 category 12 4.86 5.01 -0.156 
## 4 2 46 category 2 5.29 6.07 -0.783 
## 5 2 46 category 6 7.57 6.83 0.746 
## 6 2 46 category 12 8.29 7.96 0.324 
## 7 3 33 property 2 5.43 5.07 0.354 
## 8 3 33 property 6 4.86 4.84 0.0179
## 9 3 33 property 12 4.29 4.49 -0.200 
## 10 4 71 property 2 4.57 4.27 0.305 
## # ... with 665 more rows
```
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes %>% 
  ggplot(aes(
*   x = modelfit,
*   y = response)) +
  geom_point() 
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[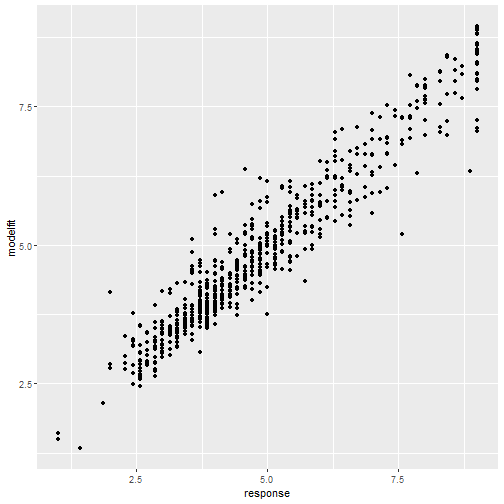
![](statistics-slides_files/figure-html/plotmodest1-1.png)
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes %>% 
  ggplot(aes(
    x = response, 
    y = modelfit)) + 
  geom_point() + 
* facet_grid(
*   condition ~ n_obs) +
  geom_abline(
    intercept = 0, 
    slope = 1)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[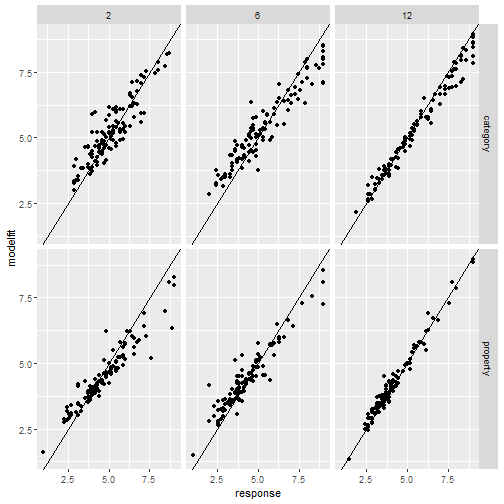
![](statistics-slides_files/figure-html/anothervis-1.png)
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes %>% 
  ggplot(aes(
*   x = response,
*   y = resid)) +
  geom_point() + 
  facet_grid(
    condition ~ n_obs) + 
  geom_hline(
    yintercept = 0)
```

A systematic misfit?
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[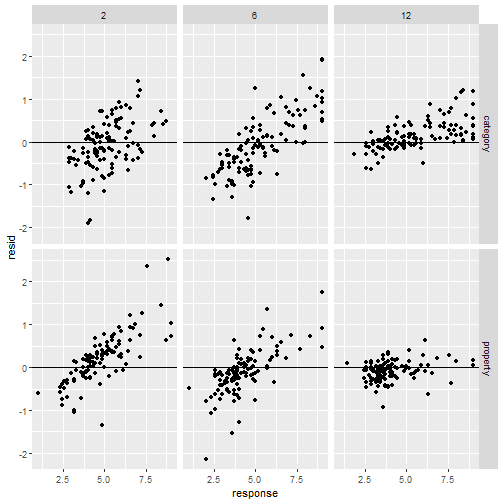
![](statistics-slides_files/figure-html/anothervis2-1.png)
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
modestframes %>%
  filter(id %in% whichids) %>%
  ggplot(aes(
*   x = n_obs, y = modelfit,
    colour = factor(id))) +
  geom_point(
    show.legend = FALSE,
    size = 4) + 
  geom_line(
    show.legend = FALSE, 
    lwd = 2,
    alpha = .3) + 
  facet_wrap(~ condition)
```

But it's a little closer!
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[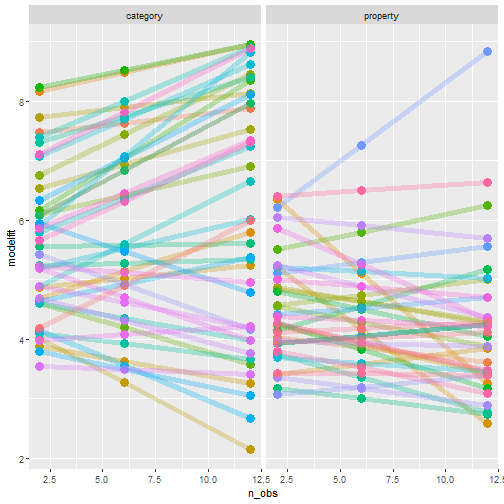
![](statistics-slides_files/figure-html/mfplot-1.png)
]]]
]]

---
class: bg-main1 center middle hide-slide-number

.reveal-text.bg-main2[.pad1[
.font4[Linear mixed models 2]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
whichids <- modestframes %>%
 pull(id) %>%
 unique() %>%
 sample(size = 20)

frames %>%
  filter(id %in% whichids) %>%
  ggplot(aes(
    x = test_item, 
    y = response, 
    shape = condition, 
    colour = factor(n_obs))) +
  geom_point(size = 2) + 
  geom_line() + 
  facet_wrap(~ id)
```

Okay, let's tackle the full data set

]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[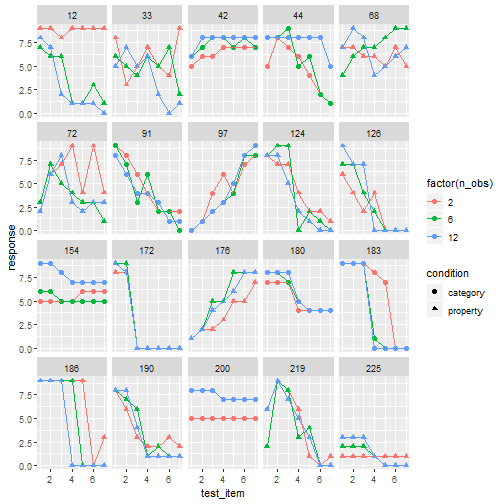
![](statistics-slides_files/figure-html/dispframes-1.png)
]]]
]]

---
class: split-40 bg-main1

.row.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[
Let's start with two sensible models:

```r
linframes1 <- lmer(formula = response ~ condition + n_obs + (1 + n_obs|id), data = frames)
linframes2 <- lmer(formula = response ~ condition + test_item + (1 + test_item + n_obs|id), 
 data = frames)

anova(linframes1, linframes2)
```
]]]
]]

--
.row[.content.vtop.center[
.pull.left[.pad1[.font2[

```
## Data: frames
## Models:
## linframes1: response ~ condition + n_obs + (1 + n_obs | id)
## linframes2: response ~ condition + test_item + (1 + test_item + n_obs | id)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq) 
## linframes1 7 23128 23173 -11556.8 23114 
*## linframes2 10 19732 19796 -9855.8 19712 3402 3 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]]]
]]

---
class: split-40 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
# store model predictions
linframes <- frames
linframes$modelfit <-
 predict(linframes2)
linframes$resid <- 
 residuals(linframes2)

# plot
linframes %>%
  filter(id %in% whichids) %>%
  ggplot(aes(
*   x = test_item, y = response,
    shape = condition, 
    colour = factor(n_obs))) +
  geom_point(size = 2) + 
  geom_line(
*   aes(y = modelfit)) +
  facet_wrap(~ id)
```
]]]
]]

.column.bg-main3[.content.vtop.center[
.pull.left[.pad1[.font2[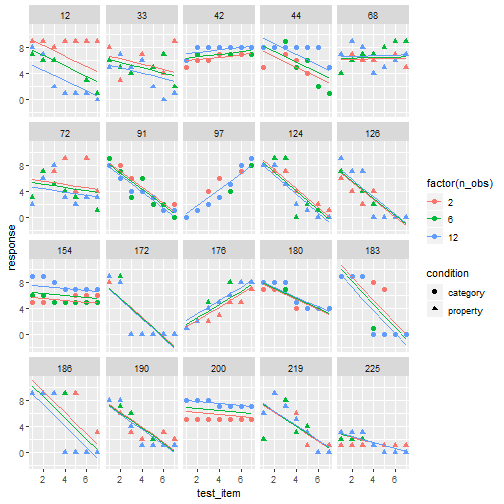
![](statistics-slides_files/figure-html/plotlmer-1.png)
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
linframes %>%
  ggplot(aes(
*   x = response,
*   y = resid)) +
  geom_point() + 
  facet_grid(
    condition ~ n_obs) + 
  geom_hline(
    yintercept = 0)
```

A systematic misfit? STILL?
]]]
]]

.column.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[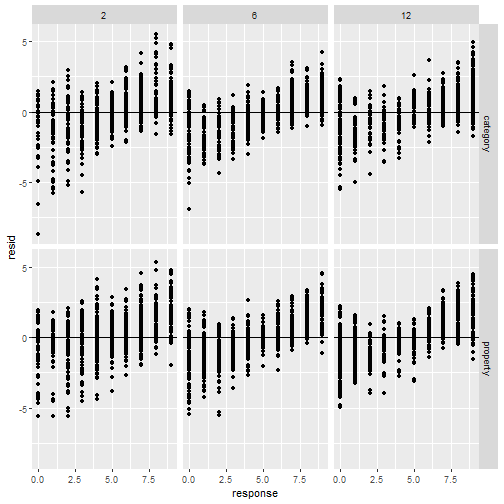

![](statistics-slides_files/figure-html/unnamed-chunk-35-1.png)
]]]
]]

---
class: split-30 bg-main1

.column.bg-main1[.content.vtop.center[

.pull.left[.pad1[.font2[

```r
linframes %>%
  ggplot(aes(
    x = response, 
    y = resid)) + 
  geom_point() + 
  facet_grid(
*   n_obs ~ test_item) +
  geom_hline(
    yintercept = 0)
```

A systematic misfit? STILL?
]]]
]]

.column.bg-main1[.content.vtop.center[
.pull.left[.pad1[.font2[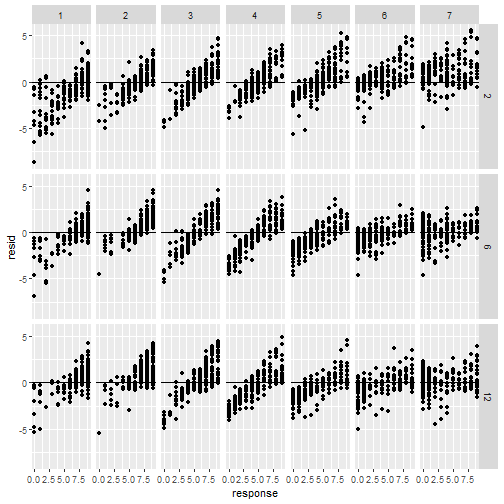

![](statistics-slides_files/figure-html/unnamed-chunk-37-1.png)
]]]
]]

---
class: bg-main1 center middle hide-slide-number

.reveal-text.bg-main2[.pad1[
.font4[Generalised linear mixed models]
]]

---

# Yeah, maybe not today...

(GLMMs allow you to fit more complicated models that can capture the nonlinearities that are causing the systematic misfits. It is briefly discussed in [the tutorial](statistics.html))

---

.pad1[.font2[
[Between the devil and the deep blue sea](https://link.springer.com/article/10.1007/s42113-018-0019-z)

.pull.left[
- .orange[Mice & tigers]. All models are *systematically* wrong. But when are they useful?
- .orange[Hindsight bias]. Model fitting is not prediction, exploration is not confirmation
- .orange[Psychometric fallacy]. Statistical modelling is not theory development...
]
]]

---

## thank you!